Basic Calculus for AI, part 3
We now can use partial derivatives to calculate rate of change in the x- and y- axes. That’s great, but the world doesn’t work in just the x- and y- axes. Sometimes one wants to know the gradient at, say, 34 degrees off x. Enter directional derivatives and the gradient vector! The directional derivative shows the gradient in any direction. The gradient vector shows the direction of the highest or lowest gradient. The latter is critical in machine learning.A.4 Directional Derivatives
A.4.1 Vectors and Unit Vectors
One needs to use a unit vector to describe the direction that one wants. Usually, one would use an angle like, \(45^\circ\) left or \(60^\circ\) right. However, since we are passing x and y variables to a function, we need to express any change in direction in terms of x and y as well. So what’s a vector?
Vector
A vector describes a line segment with direction. A line segment in 2D will have the notation \(\vec{v}=\langle{x,y}\rangle\). This means the line segment goes along the x-axis x units, and along the y-axis y units.
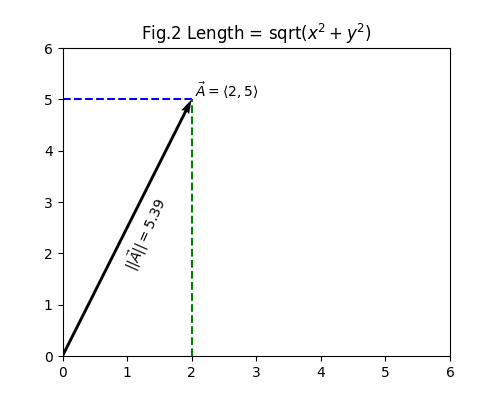
For example, say \(\vec{A} = \langle{2,5}\rangle\):

The magnitude of a vector is its length. The Pythagorean theorem takes care of that: \(\lvert\vec{v}\rvert=\sqrt{x^2+y^2}\). The pipes on either side of v may sometimes be written \(\lvert\lvert\vec{v}\rvert\rvert\) to distinguish from absolute values.
Unit Vector
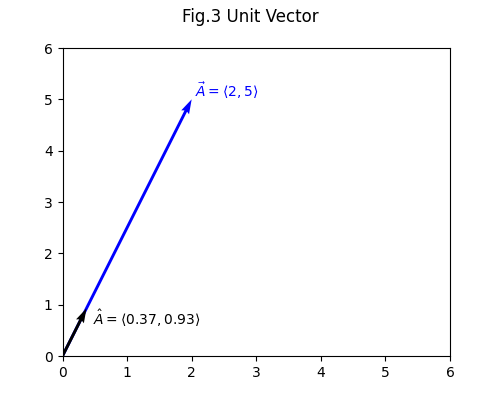
A unit vector, \(\hat{v}\), is a line segment that goes in the same direction as a vector, but has length (magnitude) 1. This is important, because we want only the unit vector to describe a change in direction without the influence of its magnitude. It is calculated by dividing the vector by its magnitude: \(\hat{v}={v\over{\lvert\vec{v}\rvert}}\)
Example
Let \(\vec{v} = \langle{2,5}\rangle\).
$$\begin{aligned} \vec{v} &= \langle{2,5}\rangle \\ \lvert\vec{v}\rvert &= \sqrt{2^2 + 5^2} \approx 5.39 \\ \hat{v} &={v\over{\lvert\vec{v}\rvert}} \approx {{\langle{2,5}\rangle}\over5.39} \\ \hat{v} &\approx \langle{{2\over5.39},{5\over5.39}}\rangle \\ \hat{v} &\approx \langle{0.37,0.93}\rangle \end{aligned}$$
A.4.2 The Gradient Vector
The partial derivatives, i.e. the gradients for the x- and y-axes, together form a vector called the gradient vector.
$$ \triangledown f(x, y) = \langle{f_x,f_y}\rangle $$
This vector accomplishes two things:
- It shows the direction of the greatest rate of change for f(x,y). The opposite direction is the greatest decrease.
- Simultaneously, its magnitude gives the greatest rate of change:\(\lvert{\triangledown f(x,y)}\rvert = \sqrt{f_x^2 + f_y^2}\).
To illustrate, I’ll use the formula I used in the last post: \(x^3y^2 + 3x^2y + 3\).
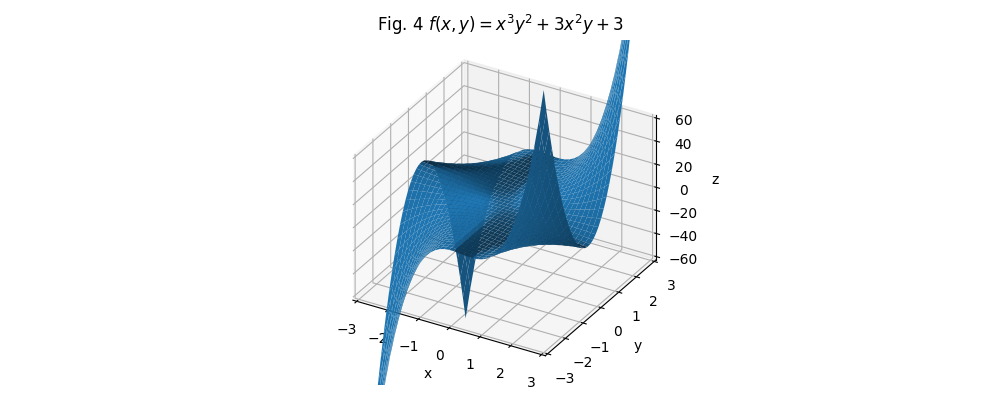
$$\begin{aligned} f(x,y) &= x^3y^2 + 3x^2y + 3 \\ f_x(x,y) &= 3x^2y^2 + 6xy \\ f_y(x,y) &= 2x^3y + 3x^2 \\ \triangledown f(x, y) &= \langle{3x^2y^2 + 6xy, 2x^3y + 3x^2}\rangle \end{aligned}$$
And to punch in, say, x=1.5 and y=0.8… $$\begin{aligned} \triangledown f(1.5, 0.8) &= \langle{11.5, 12.2}\rangle \\ \lvert\triangledown f(1.5, 0.8)\rvert &= \sqrt{11.5^2 + 12.2^2} = 16.77 \end{aligned}$$
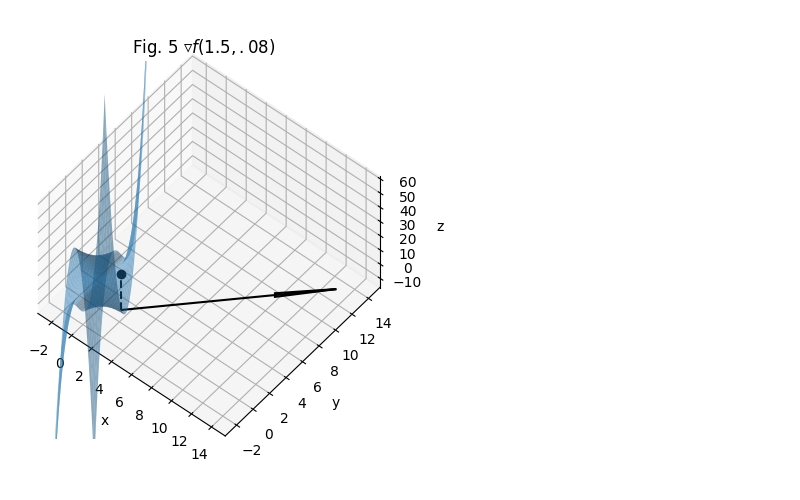
The third thing about gradient descents is that the gradient descent for a level curve is always perpendicular to the curve. This leads smart mathematicians to directional derivatives and the Lagrange Multiplier.
A.4.3 The Directional Derivative
Say we don’t want to adjust variables in the direction of the greatest change to get to a maximum. We can find the rate of change in other directions as well. We use the unit vector equivalent to trigonometry’s dot product of two vectors: \(\lvert{v}\rvert\cdot\lvert{u}\rvert\cdot\cos\theta\).
Trigonometry
Say the magnitude of \(\vec{u} = 5\) and the magnitude of \(\vec{v} = 13\). Let us say (just to make it easy on us) that they are at right angles to each other, \(90^\circ\). The magnitude of the combined angles is \(5 \cdot 13 \cdot \cos(90) = 5 \cdot 13 \cdot 0 = 0\). This makes sense, because angles completely perpendicular to each other have no influence on each other.
How about \(45^\circ\)? \(5 \cdot 13 \cdot \cos(45) = 5\cdot13\cdot0.71 = 45.96\)
Directional derivative
We can accomplish the same thing with the gradient vector and the unit vector of the direction we want to go. The equation is called the directional derivative:
$$ D_\vec{u}f(x,y) = \langle{f_x, f_y}\rangle\cdot\vec{u} $$
Say the gradient vector at point P is \(\langle{2, 5}\rangle\). The vector \(90^\circ\) to the right with the same magnitude is \(\langle{5, -2}\rangle\). The unit vector at \(90^\circ\) is, with some rounding, \(\langle{0.9275,-0.371}\rangle\). The rate of change orthogonal to our gradient vector is:
$$\begin{aligned} D_\vec{u}f(2,5) &= \langle{2, 5}\rangle\cdot\langle{0.9275,-0.371}\rangle \\ D_\vec{u}f(2,5) &= 2(0.9275) + 5(-0.371) \\ D_\vec{u}f(2,5) &= 1.855 - 1.855 \\ D_\vec{u}f(2,5) &= 0 \\ \end{aligned}$$
Next
The next posts will deal with Lagrange Multipliers and the Chain Rule.